Dos paradoxos de Zeno, o da corrida entre Aquiles e a tartaruga é porventura o mais conhecido. O herói grego Aquiles e uma tartaruga combinam uma corrida, sendo atribuída uma vantagem inicial à tartaruga. O paradoxo refere que depois desse arranque inicial da tartaruga, Aquiles não será capaz de a alcançar, pois quando chegar a uma determinada posição onde a tartaruga se encontrava antes, a tartaruga estará ligeiramente mais à frente… E assim sucessivamente.
Mas o argumento da dicotomia é mais interessante para mim. Quando se percorre uma certa distância, para chegar ao final do percurso é preciso passar primeiro pelo meio. E daí até ao final, é necessário voltar a passar pelo meio do segmento restante. Nesta sequência, nunca chegará ao final, dado que haverá sempre um ponto intermédio até lá!
A dicotomia de Zeno ao chegar ao semáforo
Este problema da dicotomia utilizo-o associado a um conceito de poupança. Quando me estou a aproximar de um semáforo e ele está vermelho, e desde que não esteja a subir, vou abrandando até chegar ao semáforo, como referi neste artigo. Na maior parte dos percursos que faço habitualmente, conheço os timings e faço uma gestão adequada da velocidade, para chegar ao semáforo com a maior velocidade potencial possível.
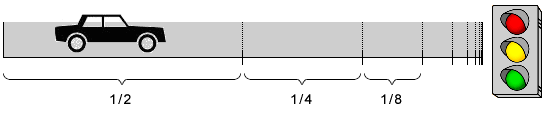
Mas quando não conheço o semáforo, ou o seu timing, e ele não é dos inteligentes, a estratégia é percorrer metade da distância até ao semáforo a uma determinada velocidade, depois reduzir essa velocidade para cerca de metade. E vou reduzindo sistematicamente a velocidade, sem nunca chegar ao semáforo. Como podem imaginar, algumas vezes o paradoxo de Zeno prega-nos partidas, e chegamos mesmo ao semáforo. Mas na maior parte das vezes, tenho sempre alguma velocidade, que serve para evitar um arranque a partir de um estado parado, o que serve naturalmente para poupar combustível.
{ 1 comment to read ... please submit second! }